Introduction

Creating sparse neural networks is a very hot topic at the moment. It is believed to make them smaller, faster and with better generalization capabilities1. For a long time however, it was believed that sparse networks were difficult to train. The traditional way of getting them was therefore to first train a dense network to convergence, then prune it to make it sparse, eventually fine-tuning it a tiny bit more to recover performance. However, some recent research has shown that not only it was possible to train sparse networks, but also that they may outperform their more-parameterized, dense, counterpart. The paper that initiated this trend talks about "lottery tickets", that may be hidden in neural networks2. In this blog post, we are going to explain what they are and how we can find them, with the help of fastai, and more particularly fasterai, a library to create smaller and faster neural networks that we created.


Lottery Ticket Hypothesis

Let's first introduce what The Lottery Ticket Hypothesis is for those who may have never heard about it. It is a fascinating characteristic of neural networks that has been discovered by Frankle and Carbin in 20192. The gist of this hypothesis can be phrased as the following:


In a neural network, there exists a subnetwork that can be trained to at least the same accuracy and in at most the same training time as the whole network. The only condition being that both this sub- and the complete networks start from the same initial conditions.


This subnetwork, called the "winning ticket" (as it is believed to have won at the initialization lottery), can be found by using pruning on the network, removing useless connections.

The steps to unveil this winning ticket are:

  1. Get a freshly initialized network, possessing a set of weights $W_0$.
  2. Train it for a certain amount $T$ of iterations, giving us the network with weights $W_T$.
  3. Prune a portion of the smallest weights, i.e. the weights that possess the lowest $l_1$-norm, giving us the network with weights $W_T \odot m$, with $m$ being a binary mask constituted of $0$ for weights we want to remove and $1$ for those we want to keep.
  4. Reinitialize the remaining weights to their original value, i.e. their value at step 1), giving us the network with weights $W_0 \odot m$.
  5. Stop if target sparsity is reached or go back to step 2).


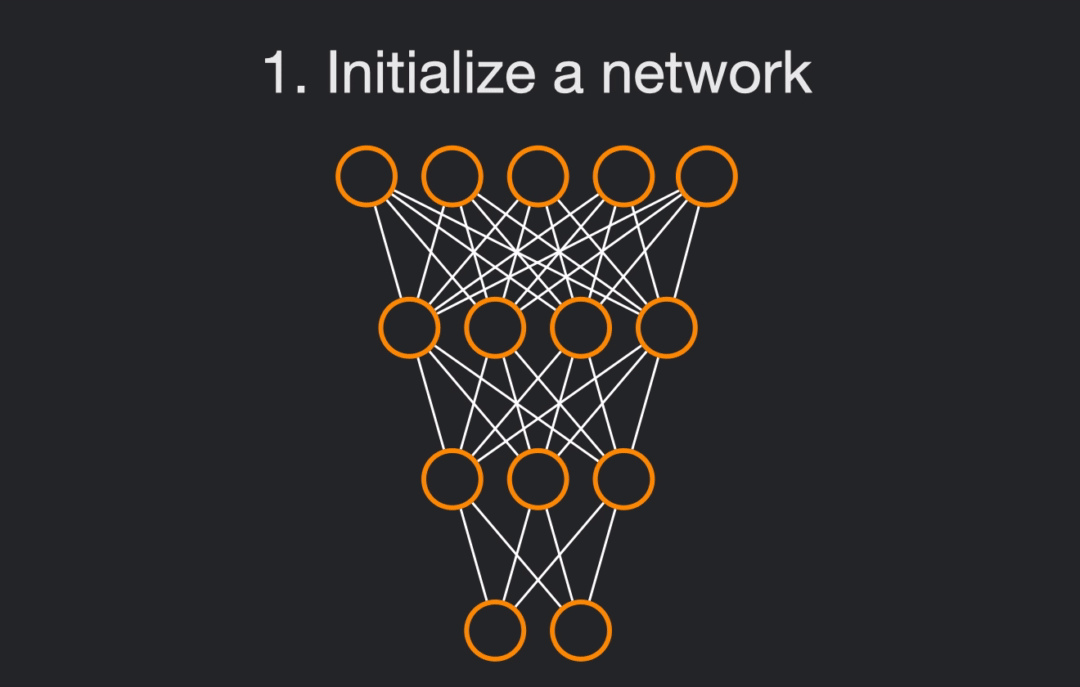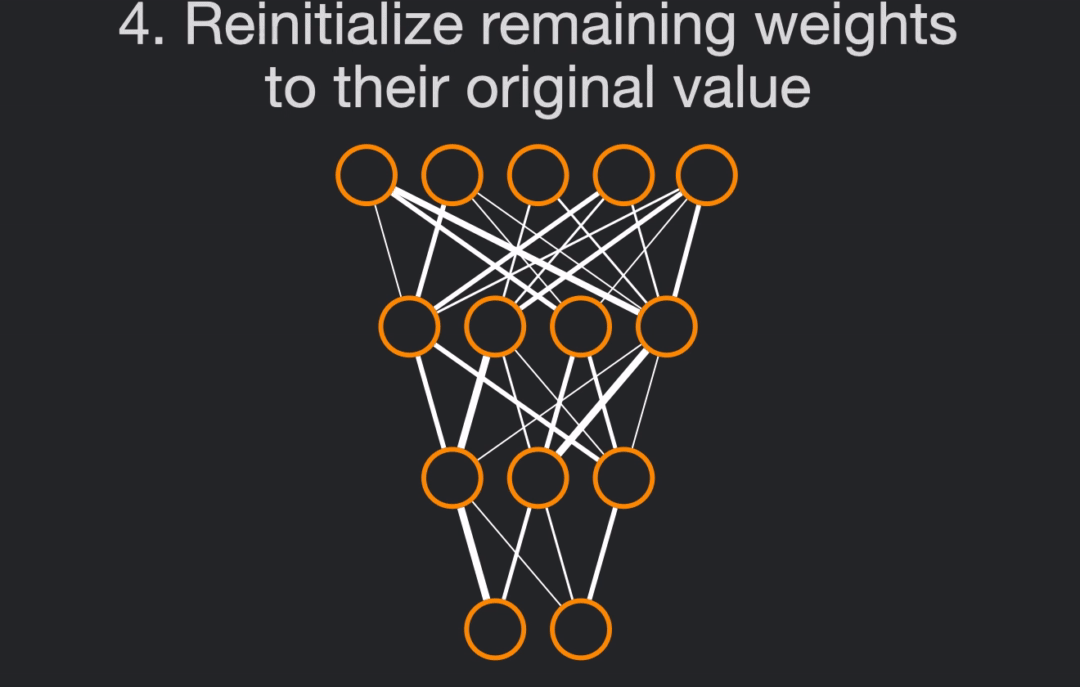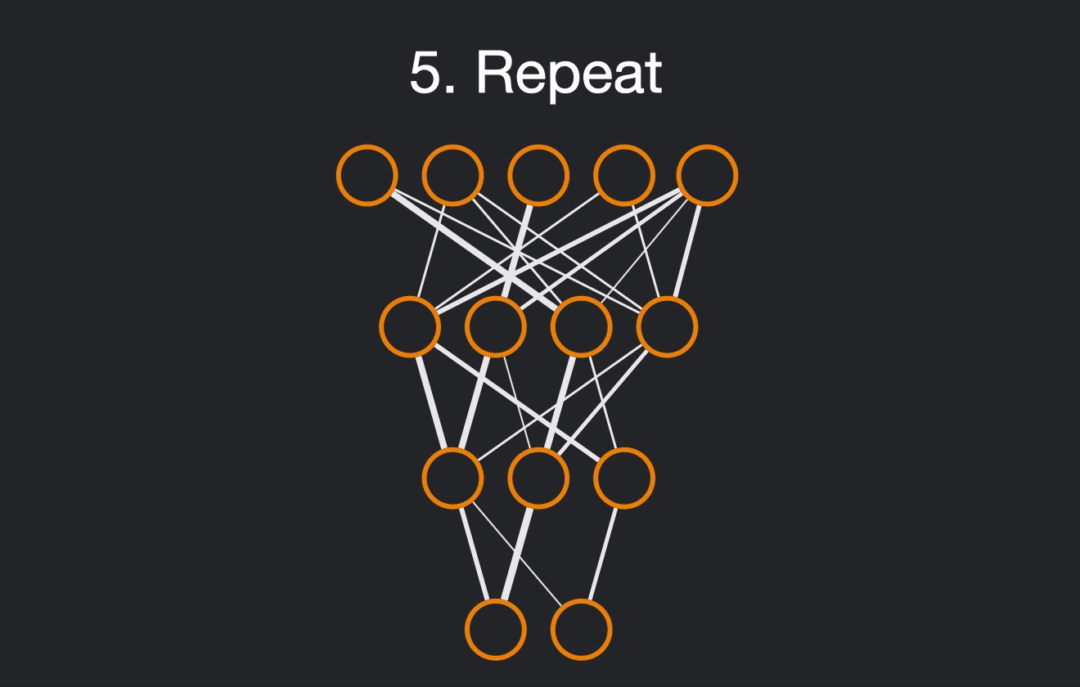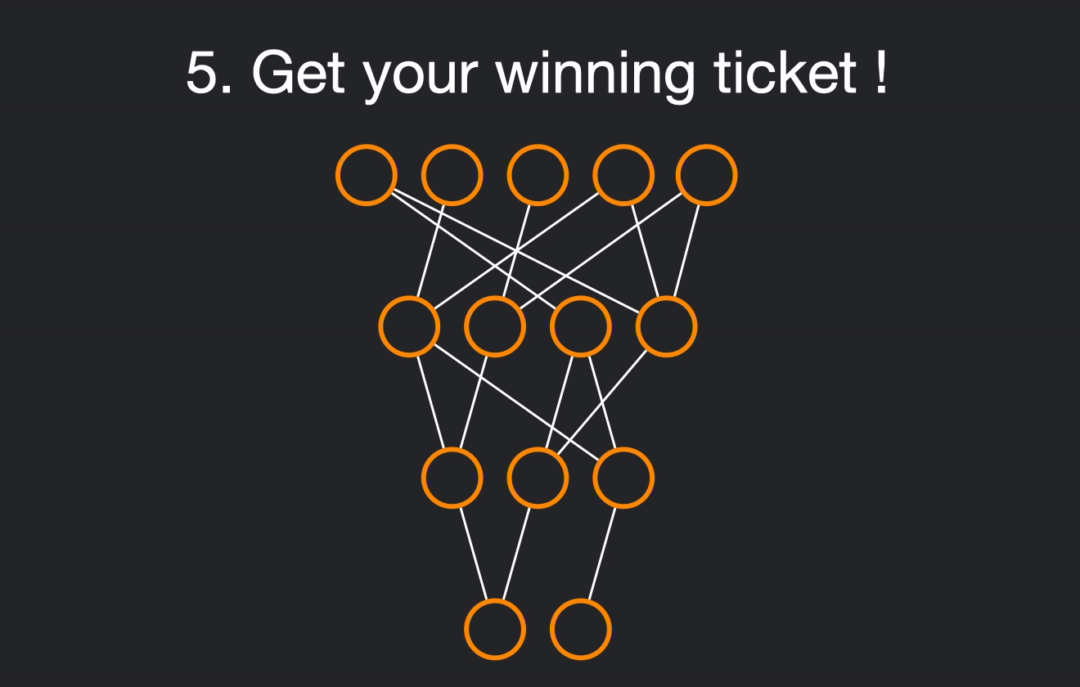
Alt Text


We will conduct this tutorial by using a ResNet-18 architecture, trained on Imagenette, a subpart of Imagenet using only 10 classes.

We first want a baseline of the complete model that we can then compare to.

learn = Learner(dls, resnet18(num_classes=10), metrics=accuracy)

Let's save the weights of this model, so that we can be sure to start from the exact same network in our further experiments.

initial_weights = deepcopy(learn.model.state_dict())

As this is our baseline, it will not be pruned. Thus, this model corresponds to $W_T$, with $T$ chosen to be $5$ epochs. So let's train it and report the final accuracy.

learn.fit(5)
epoch train_loss valid_loss accuracy time
0 1.536754 1.709699 0.481529 00:11
1 1.254531 1.314451 0.578089 00:11
2 1.116412 1.168404 0.634904 00:11
3 1.023481 1.156428 0.633376 00:11
4 0.946494 0.998459 0.677962 00:11

After training, our baseline network is $68\%$ accurate at discriminating between the 10 classes of our validation set.


Can we please find winning tickets now ?


We have already shown in a previous blog post how to prune a network with fasterai. As a quick reminder, this can be done by using the SparsifyCallback callback during training.

The only things to specify in the callback are:

  • end_sparsity, the target final level of sparsity in the network
  • granularity, the shape of parameters to remove, e.g. weight or filter
  • method, either prune the weights in each layer separately (local) or in the whole network (global)
  • criteria, i.e. how to score the importance of parameters to remove
  • schedule, i.e. when pruning is applied during training

In the original paper, authors discover tickets using an Iterative Magnitude Pruning (IMP), meaning that the pruning is performed iteratively, with a criteria based on magnitude, i.e. the $l_1$-norm of weights. Authors also specify that they remove individual weights, comparing them across the network globally.


Luckily for us, all of these were already available in fasterai! We now know most of the parameters of our callback: SparsifyCallback(end_sparsity, granularity='weight', method='global', criteria=large_final, schedule=iterative)

We are all set then ! Well almost... If you remember correctly the 5 steps presented earlier, we need to keep track of the set of weights $W_0$, at initialization. We also need to reset our weights to their initial value after each pruning step.

In fasterai this can be done by:

  • passing the lth argument to True. Behind the hood, fasterai will save the initial weights of the model and reset them after each pruning step
  • Optionnally setting a start_epoch, which affects at which epoch the pruning process will start.


Let's recreate the exact same model as the one we used for baseline.

learn = Learner(dls, resnet18(num_classes=10), metrics=accuracy)
learn.model.load_state_dict(initial_weights)

<All keys matched successfully>

In fasterai, the iterative schedule has 3 steps by default, which can easily be changed but we'll stick with it for our experiments.

We'll thus have 3 rounds of pruning, and that our network will therefor be reset 3 times. As we want the network to be trained for $T=5$ epochs at each round, this means that the total epochs over which pruning will occur is $3 \times 5 = 15$ epochs.

But before performing any round of pruning, there is first a pretraining phase of $T$ epochs. The total number of epochs is then $20$.

Let's train this bad boy and see what happens !

sp_cb = SparsifyCallback(50, 'weight', 'global', large_final, iterative, start_epoch=5, lth=True)
learn.fit(20, cbs=sp_cb)

Pruning of weight until a sparsity of 50%
Saving Weights at epoch 0
epoch train_loss valid_loss accuracy time
0 1.541520 1.568734 0.501911 00:11
1 1.258532 1.628220 0.508790 00:11
2 1.111838 1.292680 0.596688 00:11
3 1.024304 1.385538 0.581146 00:11
4 0.930883 1.041547 0.672102 00:11
5 1.330930 1.395270 0.520510 00:20
6 1.141437 1.135004 0.620637 00:20
7 1.040761 1.267395 0.581656 00:20
8 0.952175 1.272328 0.594650 00:20
9 0.909871 1.207141 0.629554 00:20
10 1.235558 1.197264 0.598217 00:20
11 1.042131 1.067109 0.658854 00:20
12 0.927392 0.977499 0.673376 00:20
13 0.888816 0.916399 0.699873 00:20
14 0.800480 0.774320 0.743439 00:20
15 1.052142 1.027188 0.665223 00:19
16 0.921996 0.945266 0.694268 00:20
17 0.831712 0.868593 0.717452 00:19
18 0.812539 1.016729 0.673376 00:19
19 0.764737 0.859072 0.725860 00:19 
Sparsity at the end of epoch 0: 0.00%
Sparsity at the end of epoch 1: 0.00%
Sparsity at the end of epoch 2: 0.00%
Sparsity at the end of epoch 3: 0.00%
Sparsity at the end of epoch 4: 0.00%
Resetting Weights to their epoch 0 values
Sparsity at the end of epoch 5: 16.67%
Sparsity at the end of epoch 6: 16.67%
Sparsity at the end of epoch 7: 16.67%
Sparsity at the end of epoch 8: 16.67%
Sparsity at the end of epoch 9: 16.67%
Resetting Weights to their epoch 0 values
Sparsity at the end of epoch 10: 33.33%
Sparsity at the end of epoch 11: 33.33%
Sparsity at the end of epoch 12: 33.33%
Sparsity at the end of epoch 13: 33.33%
Sparsity at the end of epoch 14: 33.33%
Resetting Weights to their epoch 0 values
Sparsity at the end of epoch 15: 50.00%
Sparsity at the end of epoch 16: 50.00%
Sparsity at the end of epoch 17: 50.00%
Sparsity at the end of epoch 18: 50.00%
Sparsity at the end of epoch 19: 50.00%
Final Sparsity: 50.00

As can be seen from the verbose below training results, the weights are reset to their original value every 5 epochs. This can also be observed when looking at the accuracy, which drops after each pruning round.

After each round, the sparsity level is increased, meaning that the binary mask $m$ in $W_T \odot m$ has more and more zeroes as the training goes.

The last round, performed at a constant sparsity level of $50\%$, is able to reach $72\%$ of accuracy in 5 epochs, which is better than our baseline !


Lottery Ticket Hypothesis with Rewinding

However, authors noticed that this IMP procedure may fail on deeper networks3, they thus propose to weaken the original Lottery Ticket Hypothesis, making the network to be reset to weights early in training instead of at initialization, i.e. our step 4) now resets the weights to $W_t \odot m$ with $t<T$. Such a subnetwork is no longer called a "winning" ticket, but a "matching" ticket. In this case, the regular LTH is just the particular case of $t=0$.

In fasterai, this can be done by changing the rewind_epoch value to the epoch you want your weights to be reset to, everything else stays the same. Let's try this !

learn = Learner(dls, resnet18(num_classes=10), metrics=accuracy)
learn.model.load_state_dict(initial_weights)

sp_cb = SparsifyCallback(50, 'weight', 'global', large_final, iterative, start_epoch=5, lth=True, rewind_epoch=1)
learn.fit(20, cbs=sp_cb)

Pruning of weight until a sparsity of 50%
epoch train_loss valid_loss accuracy time
0 1.529935 1.430763 0.522548 00:11
1 1.268891 1.251196 0.603822 00:11
2 1.141558 1.176961 0.626497 00:11
3 1.013069 1.312681 0.607134 00:11
4 0.933651 0.914163 0.695796 00:11
5 1.183302 1.339694 0.553121 00:20
6 1.027278 1.148169 0.634904 00:20
7 0.919856 1.031522 0.672866 00:20
8 0.890848 0.910739 0.713885 00:20
9 0.824205 0.932853 0.697580 00:20
10 1.054473 1.329592 0.585987 00:20
11 0.947696 1.136064 0.637452 00:20
12 0.852863 0.820551 0.731210 00:20
13 0.794559 1.009437 0.673631 00:20
14 0.775261 0.844786 0.721529 00:20
15 0.933353 1.198227 0.640000 00:20
16 0.846583 0.898716 0.715669 00:19
17 0.789335 0.781211 0.741656 00:20
18 0.745516 1.174927 0.637962 00:19
19 0.705972 0.786245 0.751847 00:20 
Sparsity at the end of epoch 0: 0.00%
Saving Weights at epoch 1
Sparsity at the end of epoch 1: 0.00%
Sparsity at the end of epoch 2: 0.00%
Sparsity at the end of epoch 3: 0.00%
Sparsity at the end of epoch 4: 0.00%
Resetting Weights to their epoch 1 values
Sparsity at the end of epoch 5: 16.67%
Sparsity at the end of epoch 6: 16.67%
Sparsity at the end of epoch 7: 16.67%
Sparsity at the end of epoch 8: 16.67%
Sparsity at the end of epoch 9: 16.67%
Resetting Weights to their epoch 1 values
Sparsity at the end of epoch 10: 33.33%
Sparsity at the end of epoch 11: 33.33%
Sparsity at the end of epoch 12: 33.33%
Sparsity at the end of epoch 13: 33.33%
Sparsity at the end of epoch 14: 33.33%
Resetting Weights to their epoch 1 values
Sparsity at the end of epoch 15: 50.00%
Sparsity at the end of epoch 16: 50.00%
Sparsity at the end of epoch 17: 50.00%
Sparsity at the end of epoch 18: 50.00%
Sparsity at the end of epoch 19: 50.00%
Final Sparsity: 50.00

We can see here the benefits of rewinding, as the network has reached $75\%$ in $5$ epochs, which is better than plain LTH, but also way better than the original, dense model.


Remark: The current methods return the winning ticket after it has been trained, i.e. $W_T \odot m$ . If you would like to return the ticket re-initialized to its rewind epoch, i.e. the network $W_t \odot m$, just pass the argument reset_end=True to the callback.


It thus seem to be possible to train sparse networks, and that they even are able to overperform their dense counterpart ! I hope that this blog post gave you a better overview of what Lottery Tickets are and that you are now able to use this secret weapon in your projects. Go win yourself the initialization lottery ! 🎰


If you notice any mistake or improvement that can be done, please contact me ! If you found that post useful, please consider citing it as:

@article{hubens2020fasterai,
  title   = "Winning the Lottery with fastai",
  author  = "Hubens, Nathan",
  journal = "nathanhubens.github.io",
  year    = "2022",
  url     = "https://nathanhubens.github.io/posts/deep%20learning/2022/02/16/Lottery.html"
}

References