Criteria

Which parameter is important in a neural network ?

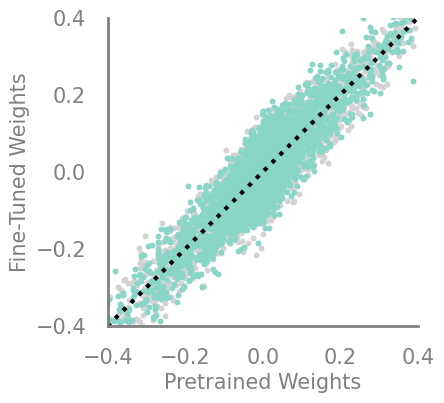
The criteria implemented come from this paper.

Weight Based Criteria

Random

demo_model(random)

Large Final Value

demo_model(large_final)

Squared Final Value

demo_model(squared_final)

Small Final Value

demo_model(small_final)

Large Init Value

demo_model(large_init)

Small Init Value

demo_model(small_init)

Large Init Large Final Value

demo_model(large_init_large_final, 80)

Small Init Small Final Value

demo_model(small_init_small_final)

Increasing Magnitude

demo_model(magnitude_increase, 60)

Movement Pruning

demo_model(movement)

Updating Versions

The following criteria use an updating value of the weights, i.e. the value from the previous iteration of training, instead of the initialization value to better capture the training dynamics.

Updating Magnitude Increase

demo_model(updating_magnitude_increase)

Updating Movement

demo_model(updating_movement, 50)

mov-magnitude

demo_model(movmag)

Updating mov-magnitude

demo_model(updating_movmag)

Gradient Based Criteria

New Ideas

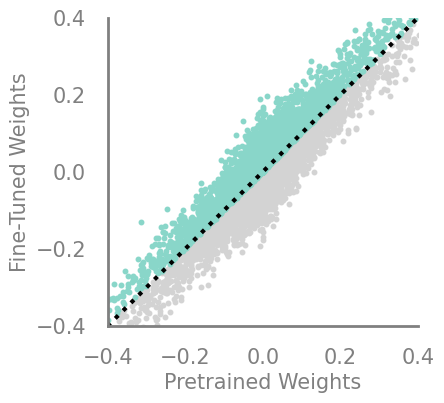
updating_magnitude_increase = Criteria(torch.abs, needs_update=True, output_f= lambda x,y: torch.abs(torch.sub(x,y)))

demo_model(updating_magnitude_increase)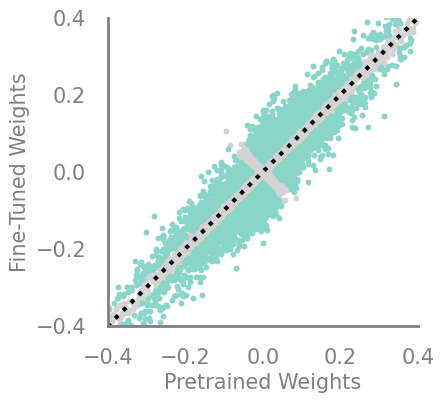

updating_magnitude_increase = Criteria(torch.abs, needs_update=True, output_f= lambda x,y: torch.sub(x,y))

demo_model(updating_magnitude_increase)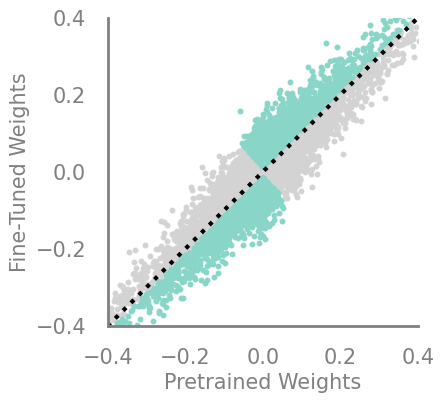

updating_magnitude_increase = Criteria(torch.square, needs_update=True, output_f= lambda x,y: torch.abs(torch.sub(x,y)))

demo_model(updating_magnitude_increase)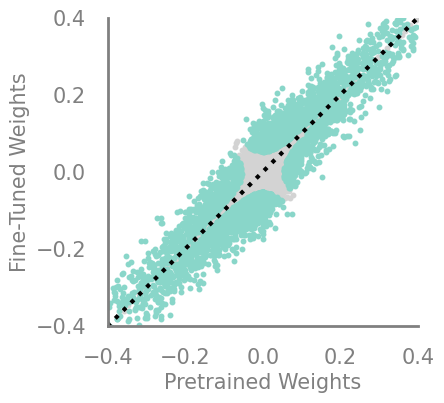

updating_movmag = Criteria(noop, needs_update=True, output_f=lambda x,y: torch.abs(torch.mul(x, torch.sub(x,y))))
demo_model(updating_movmag)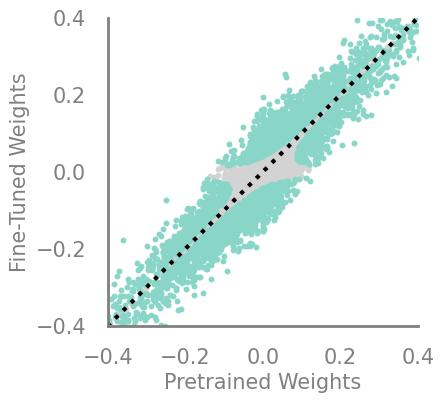

updating_movmag = Criteria(noop, needs_update=True, output_f=lambda x,y: torch.abs(torch.mul(torch.square(x), torch.sub(x,y))))
demo_model(updating_movmag)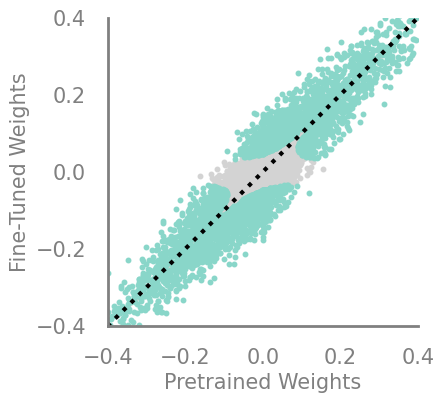

updating_movmag = Criteria(torch.square, needs_update=True, output_f=lambda x,y: torch.abs(torch.mul(x, torch.sub(x,y))))
#updating_movmag = Criteria(noop, needs_update=True, output_f=lambda x,y: torch.mul(x, torch.sub(x,y)))
demo_model(updating_movmag)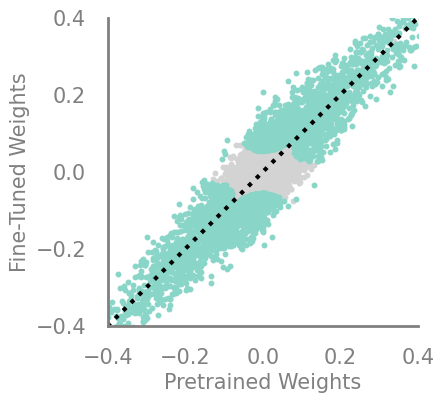

updating_movmag = Criteria(torch.abs, needs_update=True, output_f=lambda x,y: torch.abs(torch.mul(x, torch.sub(x,y))))
#updating_movmag = Criteria(noop, needs_update=True, output_f=lambda x,y: torch.mul(x, torch.sub(x,y)))
demo_model(updating_movmag, 30)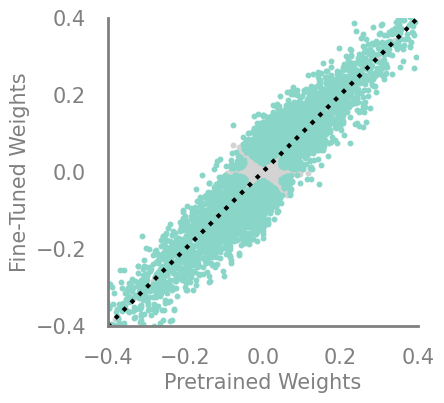

updating_movmag = Criteria(torch.abs, needs_update=True, output_f=lambda x,y: torch.mul(x, torch.sub(x,y)))

demo_model(updating_movmag, 80)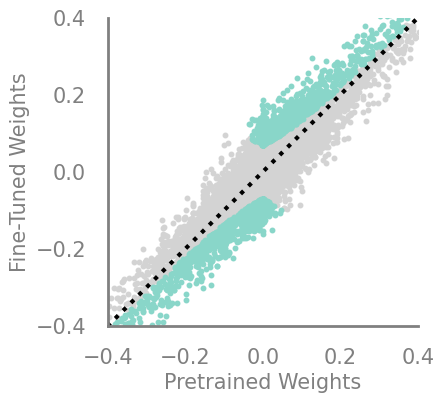

updating_movmag = Criteria(torch.square, needs_update=True, output_f=lambda x,y: torch.mul(x, torch.sub(x,y)))

demo_model(updating_movmag)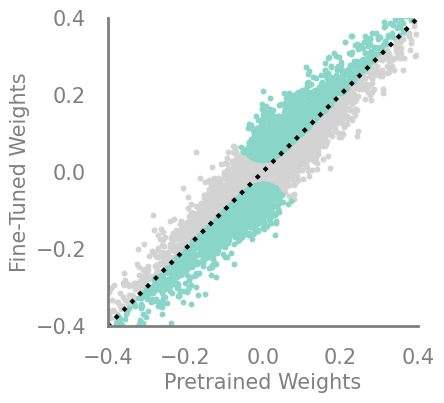

updating_movmag = Criteria(noop, needs_update=True, output_f=lambda x,y: torch.mul(x, torch.sub(x,y)))

demo_model(updating_movmag)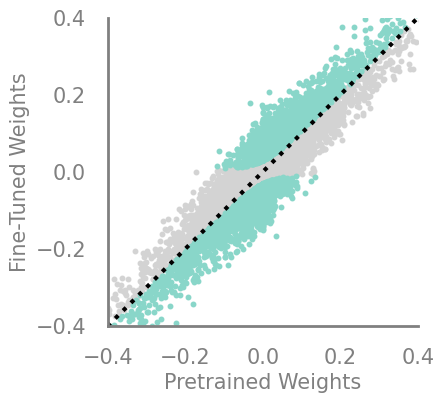

updating_movement = Criteria(noop, needs_update=True, output_f= lambda x,y: torch.abs(torch.sub(-x,y)))
demo_model(updating_movement, 50)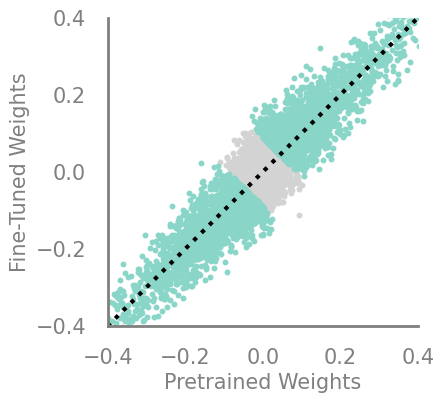

updating_movement = Criteria(torch.abs, needs_update=True, output_f= lambda x,y: torch.abs(torch.sub(-x,y)))
demo_model(updating_movement)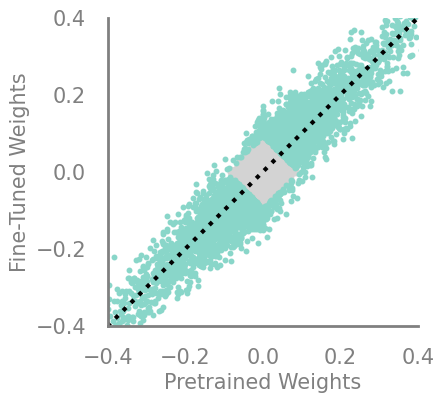

updating_movement = Criteria(torch.abs, needs_update=True, output_f= lambda x,y: torch.abs(torch.cosh(torch.sub(x,y))))
demo_model(updating_movement)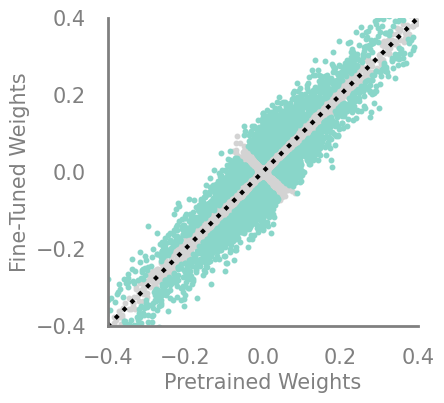

updating_movement = Criteria(torch.square, needs_update=True, output_f= lambda x,y: torch.abs(torch.sub(x,y)))
demo_model(updating_movement)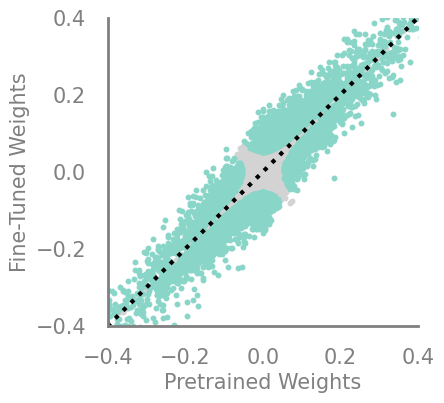

updating_movement = Criteria(noop, needs_update=True, output_f= lambda x,y: torch.sub(x,y))
demo_model(updating_movement)

mine = partial(torch.pow, exponent=4)

large_final = Criteria(torch.frac)
demo_model(large_final)