Knowledge Distillation

Train a network in a teacher-student fashion

Knowledge Distillation, sometimes called teacher-student training, is a compression method in which a small (the student) model is trained to mimic the behaviour of a larger (the teacher) model.

The main goal is to reveal what is called the Dark Knowledge hidden in the teacher model.

If we take the same example provided by Geoffrey Hinton et al., we have

The main problem of classification is that the output activation function (softmax) will, by design, make a single value really high and squash others.

\[ p_{i}=\frac{\exp \left(z_{i}\right)}{\sum_{j} \exp \left(z_{j}\right)} \]

With \(p_i\) the probability of class \(i\), computed from the logits \(z\)

Here is an example to illustrate this phenomenon:

Let’s say that we have trained a model to discriminate between the following 5 classes: [cow, dog, plane, cat, car]

And here is the output of the final layer (the logits) when the model is fed a new input image:

logits = torch.tensor([1.3, 3.1, 0.2, 1.9, -0.3])

By judging on the predictions, the model seems confident that the input data is a dog and quite confident that it is definitely not a plane nor a car, with predictions for cow and cat being moderately high.

So the model not only has learned to recognize a dog in the image, but also that a dog is very different from a car and a plane and share similarities with cats and cows. This information is what is called dark knowledge !

When passing those predictions through a softmax, we have:

predictions = F.softmax(logits, dim=-1); predictions
tensor([0.1063, 0.6431, 0.0354, 0.1937, 0.0215])

This is accuenting the differences that we had earlier, discarding some of the dark knowledge acquired earlier. The way to keep this knowledge is to “soften” our softmax outputs, by adding a temperature parameter. The higher the temperature, the softer the predictions.

soft_predictions = F.softmax(logits/3, dim=-1); soft_predictions
tensor([0.1879, 0.3423, 0.1302, 0.2294, 0.1102])
Note

if the Temperature is equal to 1, then we have regular softmax

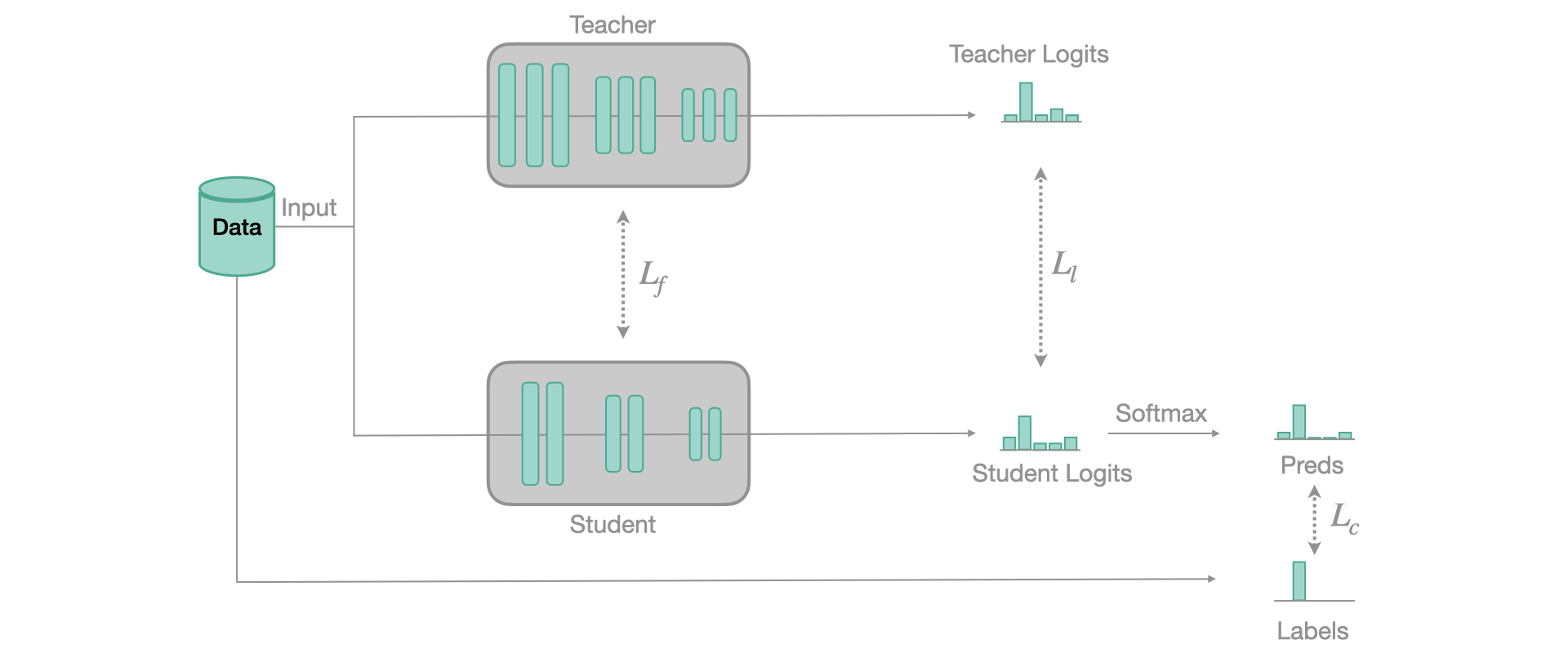
When applying Knowledge Distillation, we want to keep the Dark Knowledge that the teacher model has acquired during its training but not rely entirely on it. So we combine two losses:

The combination between those losses are weighted by an additional parameter α, as:

\[ L_{K D}=\alpha * \text { CrossEntropy }\left(p_{S}^{\tau}, p_{T}^{\tau}\right)+(1-\alpha) * \text { CrossEntropy }\left(p_{S}, y_{\text {true }}\right) \]

With \(p^{\tau}\) being the softened predictions of the student and teacher

Note

In practice, the distillation loss will be a bit different in the implementation

This can be done with fastai, using the Callback system !

KnowledgeDistillationCallback

 KnowledgeDistillationCallback (teacher, loss, activations_student=None,
                                activations_teacher=None, weight=0.5)

Basic class handling tweaks of the training loop by changing a Learner in various events

The loss function that is used may depend on the use case. For classification, we usually use the one presented above, named SoftTarget in fasterai. But for regression cases, we may want to perform regression on the logits directly.